menu
 |
 |
 |
 |
isolation, bruits
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
locaux d'écoute
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
propagation
du son dans un local |
variation
du niveau sonore en fonction de la distance à la source |
L'intensité acoustique en un point d'un local est la somme de l'intensité
de propagation directe (voir figure 2 dans absorption et
réflexion) et d'une intensité dite "diffuse",
engendrée par la somme de toutes les réflexions, indépendante
du point considéré : (théorème de superposition
ou de Béranek, le "père" américain de l'acoustique
des salles, auteur d'un ouvrage en anglais rare mais passionnant dans
lequel il analyse les plus grandes salles de concert des Etats-Unis, qu'on
peut consulter dans certaines bibliothèques universitaires)
Im(d) = Idirecte + Idiffuse Idirecte dépend de la distance Idiffuse ne
dépend que du local
En espace libre, Idirecte correspond à un niveau :
L(d) = Lw + 10 Log (1/(4pi
d2)) pi
= 3,14 |
Le
niveau sonore dépend donc a priori de
la distance (c'est la variable),
mais aussi de la géométrie et de l'absorption du
local (A
et amoyen). Dans le cas général, il dépend
aussi de la directivité Q de la source, qui elle-même dépend
de la fréquence et de la direction de l'espace. Il faut admettre
que cette formule, bien que déjà lourde, est une simplification.
En fait les sources ne sont réellement omnidirectionnelles que pour
les fréquences basses, voire très basses.
De plus, cette relation est valable pour une onde sphérique, donc
si la source est ponctuelle (ou peut y être assimilée, c'est
à dire que ses dimensions sont faibles par rapport à la géométrie
du problème, ou bien, la distance à la source est largement supérieure
à la plus grande dimension de la source), et unique (une seule source émettant
un signal donné). Ces considérations sont fondamentales
lorsqu'on s'intéresse
à la "réponse" d'une salle sonorisée. voir
: acoustique et sonorisation |
On
en déduit dans un local la relation pour une source omnidirectionnelle
:
L(d) = Lw + 10
Log (1/(4 pi d2) + 4 x (1- amoyen)/(S x amoyen))
L(d) est le niveau sonore à une distance d.
Lw est le niveau de puissance, caractéristique intrinsèque
de la source sonore, liée à sa puissance.
Pour une source ponctuelle non omnidirectionnelle, l'expression 10
Log (1/(4pi d2)) devient 10 Log (Q/(4pi d2))
dans laquelle Q
est le facteur de directivité de la source. |
|
diminution
du niveau jusqu'à la " Distance critique"
|
Loi
théorique de diminution du niveau sonore dans un local :
• valable si source ponctuelle, local de forme simple, assez régulière,
répartition homogène des matériaux de surface, ne
tient pas compte de l'absorption de l'air, ni des phénomènes
d'ondes stationnaires.
La distance est ici en échelle log, ce qui facilite la représentation,
mais est moins "parlant", la distance est une notion humainement
linéaire;
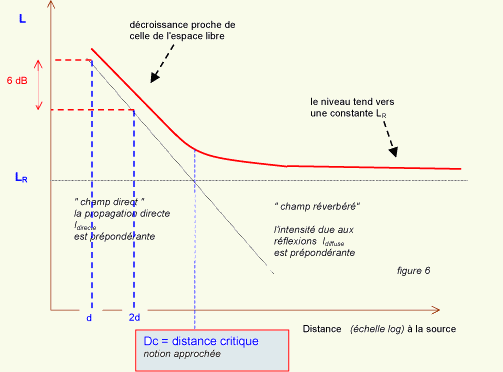
- près
de la source sonore, le niveau diminue presque comme en espace libre
(loi log 6 dB par doublement de la distance)
- loin
de la source, le niveau tend vers une valeur constante Lr.
On
peut simplifier et considérer 2 zones :
- décroissance dans le "champ
direct"
- niveau
constant dans le "champ réverbéré"
- distance "critique" Dc
= limite entre ces 2 zônes,
suffit à caractériser simplement les phénomènes.
|
l'allure
de la décroissance dépend
de l'absorption
|
|
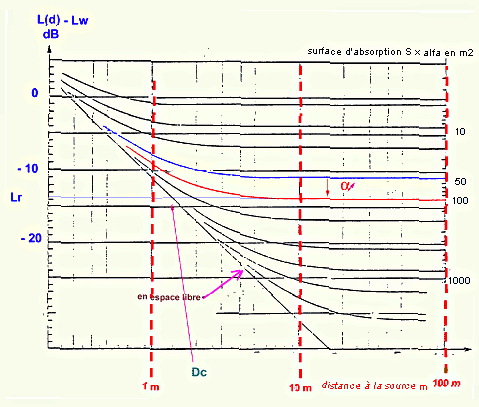
La
quantité représentée ici est L(d) - Lw., ce qui explique
les valeurs négatives. C'est en fait L(d) à une constante
près. Lorsqu'on fait varier Lw (en parlant plus fort ou en augmentant
le volume …) on ne change rien à la forme de la courbe,
on ne fait que faire varier la constante Lw.
La diminution du niveau sonore en fonction de la distance dans un local
dépend, au delà de la distance critique Dc, de la surface
d'absorption.
Une augmentation de l'absorption diminue le niveau loin de la source
(comparer courbes bleue et rouge). Cette diminution reste plutôt faible :
entre courbe bleue et rouge, - 3 dB avec environ multiplication par 2
de la surface d'absorption. Autre conséquence : augmentation de
la distance critique.
Cette loi
n'est pas valable à proximité immédiate (moins de 1 mètre
environ) des parois. Elle ne tient pas compte, comme précisé
plus haut, de l'absorption de l'air (non négligeable aux fréquences
élevées), ni des phénomènes d'ondes stationnaires
(remarquables surtout aux fréquences basses). Bien sûr il
y a dans un local une distance maximum possible selon ses dimensions!
|
Quand
on à affaire à un problème de nuisance, on pourrait
espérer diminuer le bruit par une augmentation de l'absorption
: les moyens à mettre en œuvre sont importants pour une efficacité
relativement faible : à réserver aux bruits émis
dans le même local, si on n'a pas d'autre solution, et si l'absorption
est faible (donc réverbération élevée) au
départ. Sans oublier que cette efficacité n'existe de toutes
façons que suffisamment loin de la source.
Si on connaît le niveau en un point, par exemple à 1 mètre,
on peut utiliser ce graphe comme abaque de détermination du niveau en
n'importe quel autre point dans la même direction, ou en toutes directions
si la source est vraiment omnidirectionnelle, ou encore pour
étudier l'influence d'une modification de l'absorption. voir : traitement
acoustique |
L'application excel / open office propag.xls
en page calculs permet
d'étudier
la variation de la courbe de propagation en fonction de valeurs diverses
des paramètres :
- niveau de puissance
et directivité de
la source,
- réverbération et dimensions du local
|
|
|
|
Réalisé par Patrick Carré, ingénieur INSA, ancien acousticien conseil et prof acoustique Université Lyon
1
contact : 
La reproduction de tout ou partie de ce site sur tout document papier ou numérique est formellement interdite sauf avec l'autorisation de l'auteur, et sauf fiches pratiques |
|